Replicate Weights in the Current Population Survey

Go Back to IPUMS-CPS Documentation

Summary

What are replicate weights?

Replicate weights are currently available for the 2005-Onward Annual Social and Economic Supplement (ASEC) to the Current Population Survey. In the CPS, there are 160 separate weights at the household and person levels that allow users to generate empirically derived standard error estimates. These standard errors can then be used in hypothesis testing and in the construction of confidence intervals around the sample estimate of interest.

Why might I want to use replicate weights?

In theory, the standard error of an estimate measures the variation of a statistic across multiple samples of a given population. Thus the true standard error of any characteristic calculated from a single sample can never be known with certainty; sample standard errors are simply estimated. Replicate weights allow a single sample to simulate multiple samples, thus generating more informed standard error estimates that mimic the theoretical basis of standard errors while retaining all information about the complex sample design. These standard errors can then be used to obtain more precise confidence intervals and significance test.

Does using replicate weights make any substantive difference?

In IPUMS testing of CPS data, replicate weights usually increase standard errors. This increase is generally not large enough to alter the significance level of coefficients, though marginally significant coefficients may become clearly nonsignificant. The more obvious effect of using replicate weights is on the width of confidence intervals, which can change substantially.

How do I obtain replicate standard errors from IPUMS-CPS data?

There are 3 main steps:

  1. Run your analysis using the full-sample weights for ASEC (ASECWT and HASECWT are the main CPS ASEC weights). Record the statistic you are interested in (e.g., the mean income of veterans, or the coefficient describing the relationship between income and whether one has health insurance coverage).
  2. Run your analysis again using each set of replicate weights. First, run the analysis using REPWTP1, then again using REPWTP2, then again using REPWTP3, and so on up to the final set of replicate weights. After each set, record the statistic you are interested in. (N.B.: If you are analyzing a household-only file, be sure to use REPWT1, REPWT2, etc.)
  3. Insert the above results into the following formula:
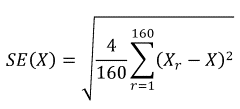
    Replicate Weight Formula
    where X is the result from the analysis using the full-sample weight and Xr is the result from the analysis using the r-th set of replicate weights.

Is there any way to do this automatically in major statistical packages?

Yes. Although the replicate standard errors contained in the IPUMS-CPS data are calculated using the a combination of the successive difference replication and modified half-sample methods, which are different from the types of replicate weights that most statistical software packages can handle, Stata can process IPUMS-CPS replicate weights automatically as of version 11.1 (released June 3, 2010).

To use IPUMS-CPS replicate weights in R, you must use the srvyr package.

install.packages("srvyr")
library("srvyr")

Next, you'll create a survey object using the replicate weights. The as_survey_rep function has other arguments you can customize if needed.

svy <- as_survey_rep(data,
					weight = ASECWT,
					repweights = matches("REPWTP[1-9]+"))

Any calculations you'd like to make with the replicate weights can be done with the object 'svy' instead of the object 'data'.

To use IPUMS-CPS replicate weights in Stata, you must first svyset the data.

. svyset [iw=ASECWT], sdrweight(repwtp1-repwtp160) vce(sdr) mse

Earlier versions of Stata can also handle successive difference replicate weights. Correspondence with StataCorp statisticians and IPUMS testing revealed that successive difference replicate weights can be treated as jackknife replicate weights if the options are specified correctly.

The svyset command for Stata versions 11.0 and before is slightly different:

. svyset [iw=ASECWT], jkrweight(repwtp1-repwtp160, multiplier(.025)) ///
	  	vce(jackknife) mse

After svysetting the data, you run the command using the svy: prefix, which passes along the options you defined above.

. svy: command

Stata will execute this command using the full-sample weights and again for each set of replicate weights. There are two important things to note:

As of March 2010, SAS (version 9.2) and PASW/SPSS (version 18.0) cannot handle successive difference replicate weights. SPSS does not allow for replicate-based variance estimation unless it performs the resampling itself, and SAS's jackknife procedure (available in PROC SURVEYREG and related statements) does not contain the options needed to mimic the above formula. See the Census Bureau's "Estimating ASEC Variances with Replicate Weights" document for sample SAS code that can be adapted to calculate replicate standard errors manually.

Can I simply divide the full sample into 160 random subsamples from the full sample and calculate replicate standard errors manually?

No. Replicate weights contain full information about the complex sample design of the CPS, and this information would be lost when drawing random subsamples. Furthermore, replicate samples incorporate information from all cases in the full sample. In contrast, random subsamples would each be 1/160th the size of a single replicate subsample.

How are the CPS replicate weights calculated?

As mentioned, replicate weights in the CPS are constructed using the successive difference replication method (for cases in self-representing strata) and the modified half-sample technique (for cases in non-self-representing strata). Both involve creating a k x k Hadamard matrix (where k is the number of replicate weights desired), assigning sample cases to rows in the matrix and calculating a replicate factor from the row values, and finally multiplying the full-sample weight by these replicate factors. The replicate samples then undergo the same weighting procedures as the full sample--adjustments for noninterivews, oversampling, and the like. For more details, see the Census Bureau's "Estimating ASEC Variances with Replicate Weights" document as well as the following:

Back to Top